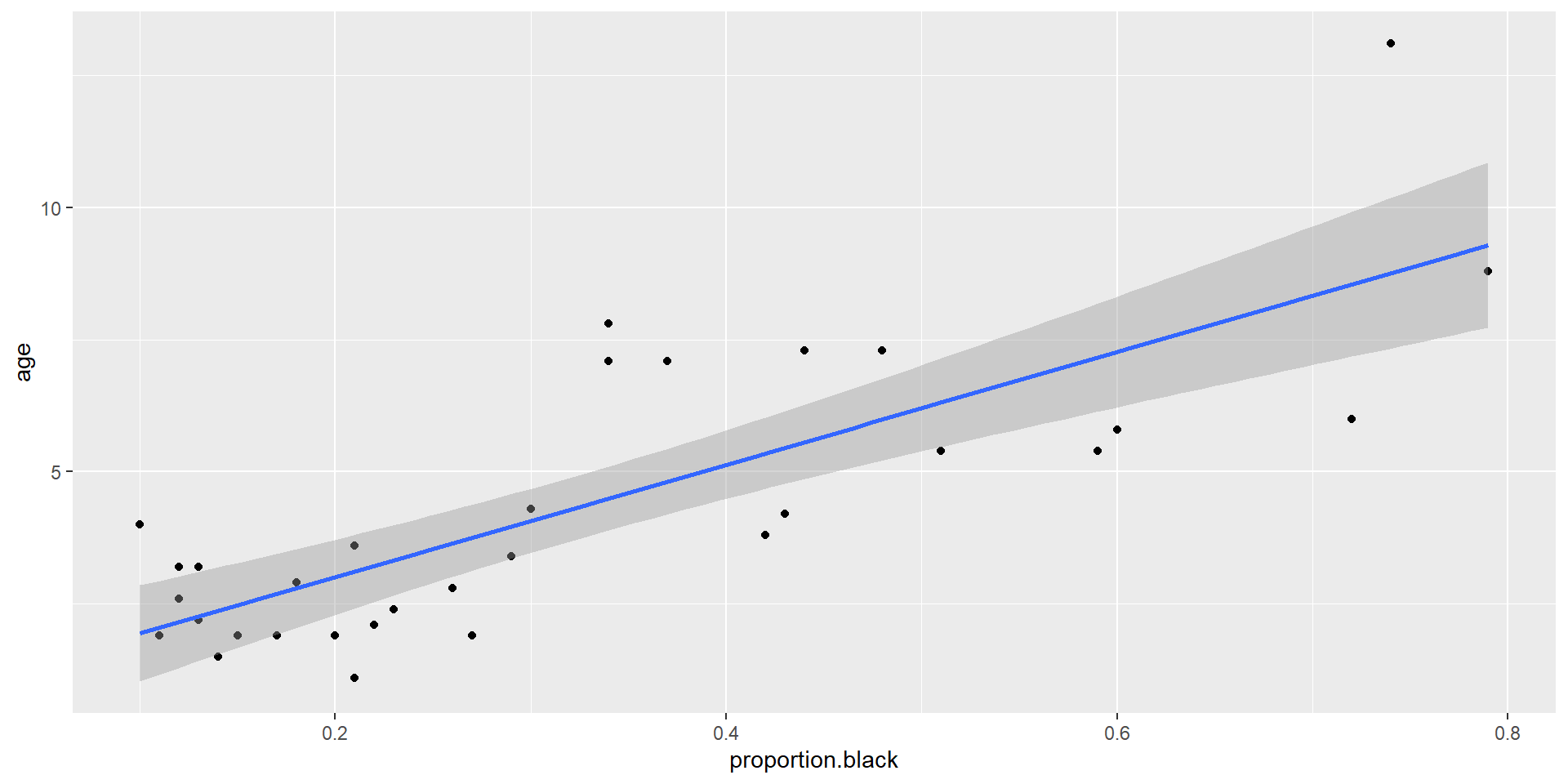
ggplot(LionNoses, aes(proportion.black, age)) + geom_point() +
geom_smooth(method = "lm")Partial regression and partial residual plots
Learning Objective
Understand approaches for visualizing fitted multiple regression models
Visualizing Simple Linear Regression
Multiple regression
Multiple regression
Call:
lm(formula = clutch ~ year + date, data = clutch.r)
Residuals:
Min 1Q Median 3Q Max
-3.2815 -0.6219 -0.2235 0.6514 3.9304
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.852483 0.757991 20.914 < 2e-16 ***
year1998 -0.344801 0.287552 -1.199 0.233
year1999 -0.125952 0.274168 -0.459 0.647
date -0.041478 0.005904 -7.026 1.07e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.288 on 130 degrees of freedom
Multiple R-squared: 0.2789, Adjusted R-squared: 0.2623
F-statistic: 16.76 on 3 and 130 DF, p-value: 2.889e-09Visualizing Multiple Regression
\[Clutch_i \sim N(\mu_i, \sigma^2)\] \[\mu_i = \beta_0+\beta_1I(Year = 1998)_i + \beta_2I(year = 1999)_i + \beta_3date_i\]
\(\beta_3\) reflects the “effect” of nest initiation date after accounting for year.
How can we visualize this “effect”?
- Added variable or partial plots
- Component + residual or partial plots
See the paper by Larano and Corcobado (2008) and Section 3.14 in the Book.
Added Variable Plots (for \(X_i\))
- Regress \(Y\) against \(X_{-i}\) (i.e., all predictors except \(X_i\)), and obtain the residuals
- Regressing \(X_i\) against all other predictors (\(X_{-i}\)) and obtain the residuals
- Plot the residuals from [1] against the residuals from [2].
Plots the part of \(Y\) not explained by other predictors (i.e., \(X_{-i}\)) against the part of \(X_i\) not explained by the other predictors (\(X_{-i}\)).
Lets us visualize the effect of \(X_i\) after accounting for all other predictors.
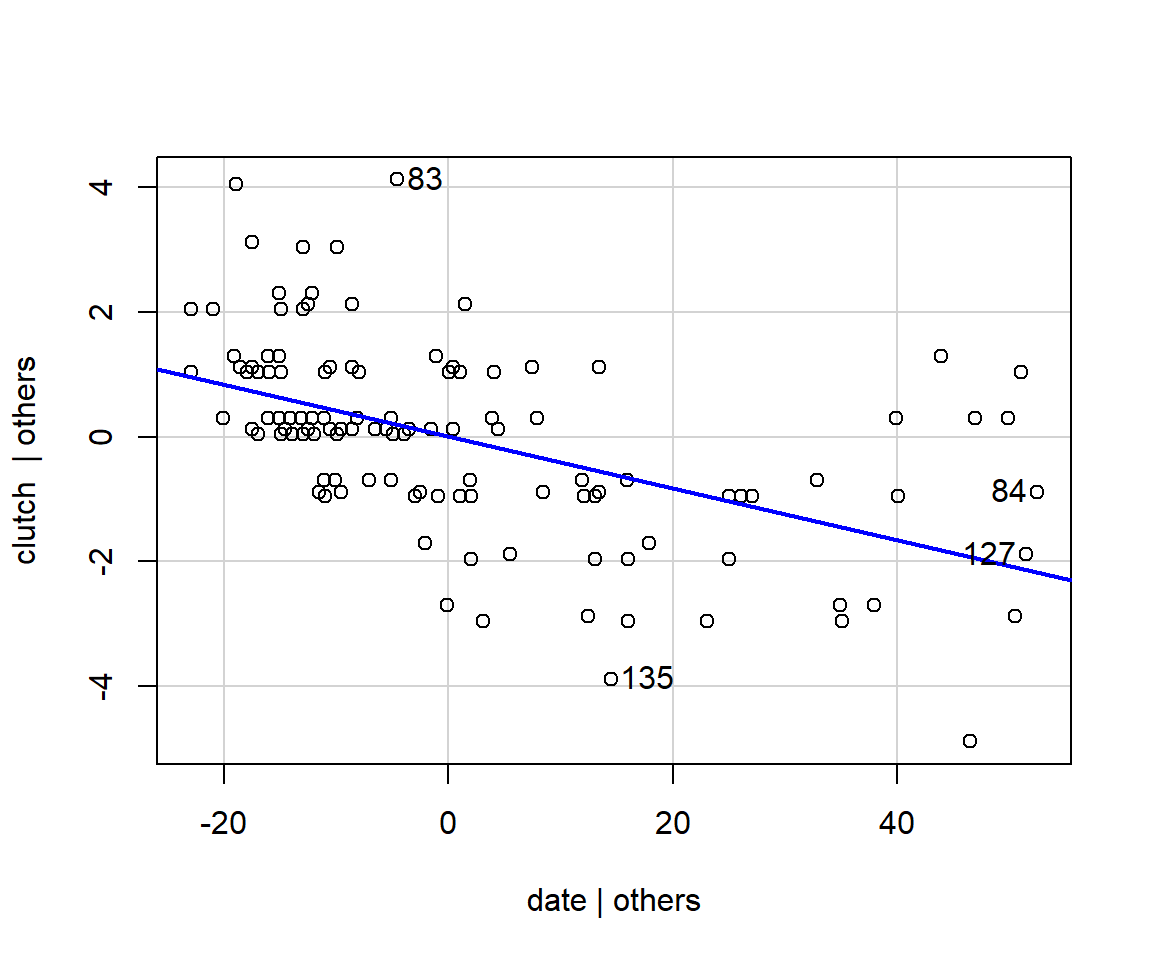
- Shows the slope and the true scatter of points around the partial line in an analogous way to bi-variate plots in simple linear regression
- Tells us about the importance of \(X_2\) (given everything else already in the model)
- Can help with diagnosing non-linearities
- Helps visualize influential points and outliers
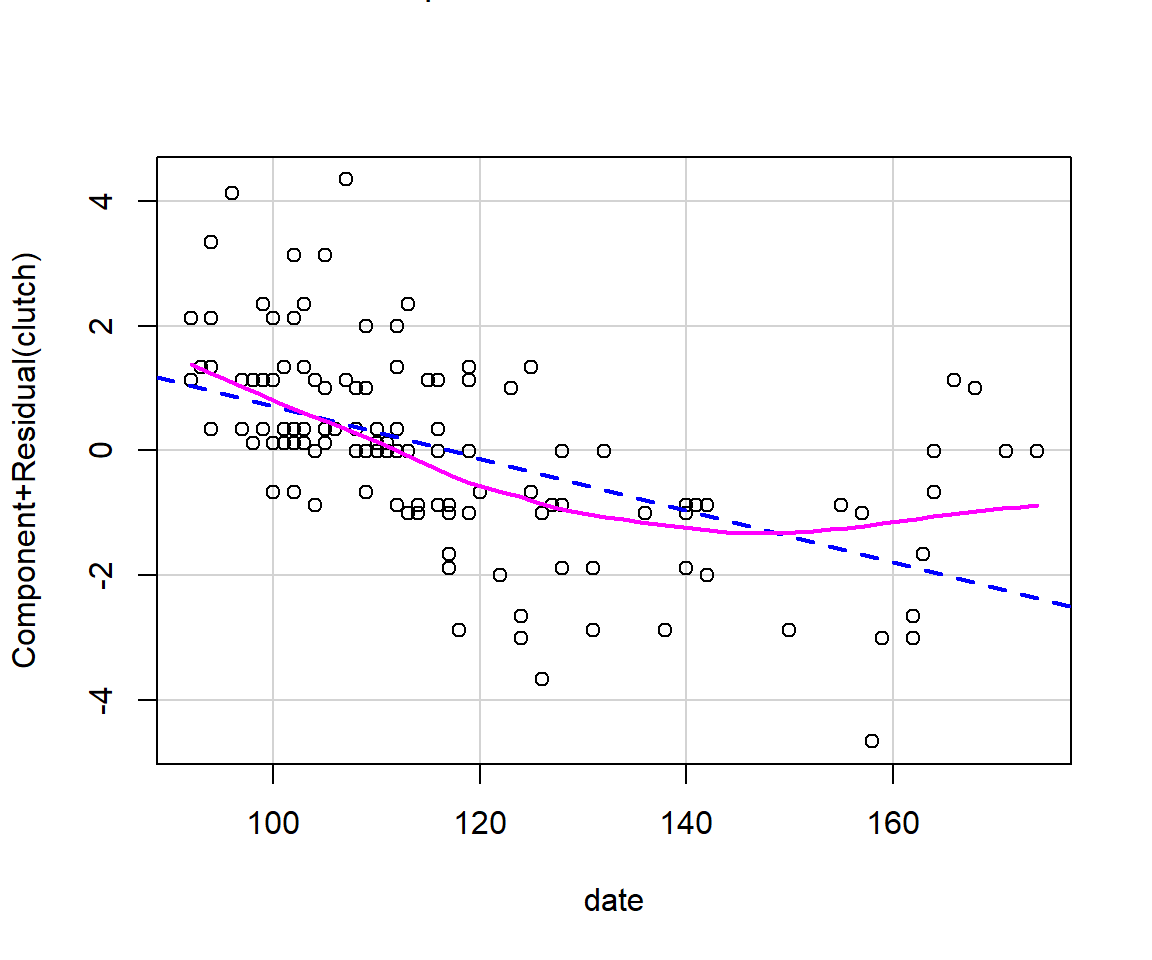
Component + residual plots or partial residual plot
Plots \(X_i\beta_i + \hat{\epsilon}_i\) versus \(X_i\).
- Better for diagnosing non-linearities
- X-axis depicts the scale of the focal variable (rather than the scale residuals)
- Not as good at depicting the amount of variability explained by the predictor (given everything else in the model).
- Easy to generalize to other regression models (see visreg package on Canvas)
Component + residual plot
Effect plots
See Section 3.14.3 in the Book. Consider a focal predictor \(X_i\) and the set of all other predictors \(X_{-i}\).
We can plot adjusted means by varying a focal variable over its range of observed values, while holding all non-focal variables at constant values (e.g., at their means or modal values).
Depict \(E[Y_i | X_{-i} = x_{-i}]\) versus \(X_i\).
Alternatively, we can plot marginal means. These are formed in much the same way, except that predictions are averaged across different levels of each categorical variable.
These two types of means are equivalent if there are no categorical predictors in the model.