Generalized Least Squares

FW8051 Statistics for Ecologists

Learning Objectives

Learn how to use generalized least squares (GLS) to model data where \(Y_i|X_i\) is normally distributed, but the variance of the residuals is not constant and may depend on one or more predictor variables.

Generalized Least Squares

Can be used to model data where \(Y_i | X_i\) is normally distributed, but we have:

• Non-constant variance (Chapter 5)

• Data that are correlated
  • Multiple measurements on the same sample unit (Chapter 18)
  • Temporal dependence (Chapter 6 of Zuur et al)
  • Spatial dependence (Chapter 7 of Zuur et al)

For this class, we will focus on non-constant variance and multiple measurements on the same sample unit [later in the course]

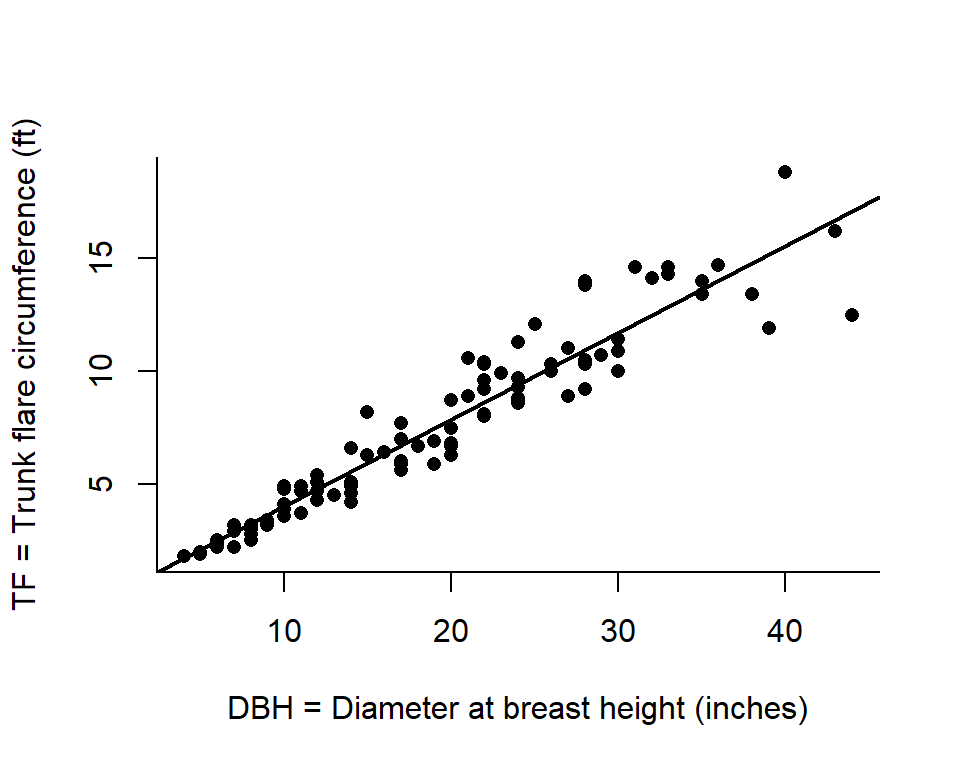
Trunk Flare Diameter

Eric North, PhD (former FW8051 student and urban forester).

Linear Model

\(Y_i = \beta_0 + X_i\beta_1 + \epsilon_i\)

Assume \(\epsilon_i\) are independent, normally distributed, with constant variance.

\(\epsilon_i \stackrel{iid}{\sim} N(0, \sigma^2)\)

\(iid\) = independent and identically distributed

\[Y_i \sim N(\mu_i, \sigma^2)\]

\[\mu_i= \beta_0 + X_i\beta_1\]

Generalized Least Squares: Non-Constant Variance

\[Y_i \sim N(\mu_i, \sigma_i^2)\]

\[\mu_i= \beta_0 + X_i\beta_1\]

\[\sigma^2_i \sim f(X_i; \tau)\]

Model the mean and variance:

• \(E[Y_i|X_i] = \mu_i = \beta_0 + X_i\beta_1\)
• \(Var[Y_i|X_i] = \sigma^2_i = f(X_i; \tau)\), where \(\tau\) are additional variance parameters.

Generalized Least Squares: Non-Constant Variance

\[Y_i \sim N(\mu_i, \sigma_i^2)\]

\[\mu_i= \beta_0 + X_i\beta_1\]

\[\sigma^2_i \sim f(X_i; \tau)\]

• the variance depends on the level of a categorical variable, \(g\)
  • varIdent: \(\sigma^2_i = \sigma^2_g\)
• the variance scales with a continuous covariate, \(X\)
  • varFixed: \(\sigma^2_i = \sigma^2X_i\)
  • varPower: \(\sigma^2 |X_i|^{2\delta}\)
  • varExp: \(\sigma^2e^{2\delta X_i}\)
  • varConstPower: \(\sigma^2 (\delta_1 + |X_i|^{\delta_2})^2\)
• the variance depends on the mean
  • varPower(form = ~ fitted(.)): \(\sigma^2_i= \sigma^2\mu_i^{2\theta} = \sigma^2(\beta_0 + X_{1i}\beta_1 + X_{2i}\beta_2 + \ldots X_{pi}\beta_p)^{2\theta}\)

T-test with unequal variances: Jaw data

males<-c(120, 107, 110, 116, 114, 111, 113, 117, 114, 112)
females<-c(110, 111, 107, 108, 110, 105, 107, 106, 111, 111)
jawdat <- data.frame(jaws = c(males, females),
                     sex = c(rep("M",10), rep("F", 10)))

boxplot(jaws~sex, data=jawdat)

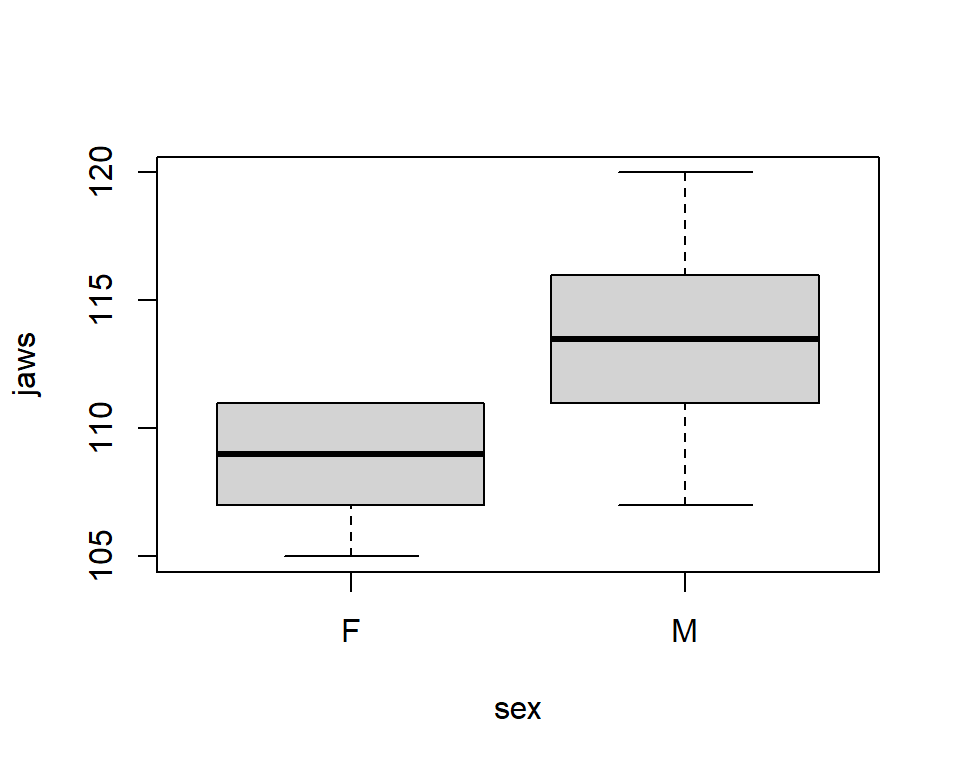
T-test with unequal variances: Jaw data

\(Y_i\) = jaw length for jackal \(i\)

\[\begin{gather} Y_i \sim N(\mu_{i}, \sigma^2_{i}) \\ \mu_i = \beta_0 + \beta_1 \text{I(sex=male)}_i \\ \sigma_i^2 = \sigma^2_{sex} \end{gather}\]

gls_ttest <- gls(jaws ~ sex, 
                 weights = varIdent(form = ~ 1 | sex), 
                 data = jawdat)

Estimates of regression parameters are obtained by minimizing:

\[\begin{gather} \sum_{i = 1}^n \frac{(Y_i - \mu_i)^2}{2\sigma^2_i} \nonumber \end{gather}\]

summary(gls_ttest)

Generalized least squares fit by REML
  Model: jaws ~ sex 
  Data: jawdat 
       AIC      BIC    logLik
  102.0841 105.6456 -47.04206

Variance function:
 Structure: Different standard deviations per stratum
 Formula: ~1 | sex 
 Parameter estimates:
        M         F 
1.0000000 0.6107279 

Coefficients:
            Value Std.Error   t-value p-value
(Intercept) 108.6 0.7180211 151.24903  0.0000
sexM          4.8 1.3775993   3.48432  0.0026

 Correlation: 
     (Intr)
sexM -0.521

Standardized residuals:
        Min          Q1         Med          Q3         Max 
-1.72143457 -0.70466511  0.02689742  0.76657633  1.77522940 

Residual standard error: 3.717829 
Degrees of freedom: 20 total; 18 residual

Summary output

Apparent parameterization:

\(\sigma^2_{sex} = \sigma^2\delta^2_{sex}\), which is the same as \(\sigma_{sex} = \sigma\delta_{sex}\)

with:

• \(\hat{\delta}_{males}=1\)
• \(\hat{\delta}_{females} = 0.61\)
• \(\hat{\sigma} = 3.72\) (residual standard error)

Actual Parameterization

Variance model parameterization actually looks like a linear model on the log scale:

\(log(\sigma_i) = \gamma_0 + \gamma_1\text{I(sex = female)}_i\)

Ensures that \(\sigma_i\) is positive when we back-transform using exp().

Actual parameterization used by R:

\(log(\sigma_i) = log(\sigma) + log(\delta)\text{I(sex = female)}_i\)

Which is the same as:

\(\sigma^2_i = \sigma^2 \delta^{2\text{I(sex=female)}}\)

(see book for details)

Fraser River Sockeye

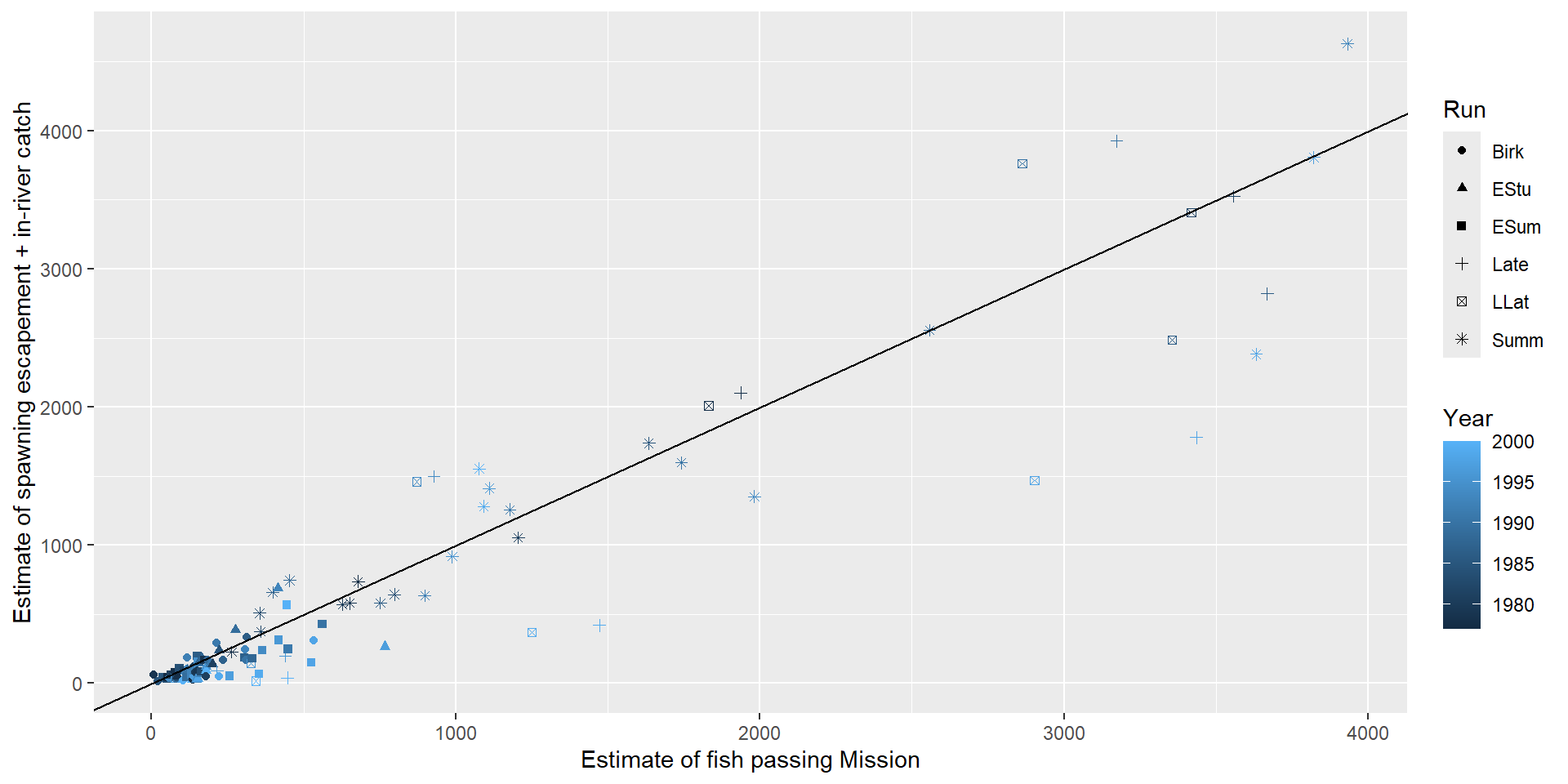
Use historical correlation between the count at Mission and \(S_t + C_t\) to manage the fishery

Variance increasing with \(X_i\) or \(\mu_i\)

1. Fixed variance model: \(\sigma^2_i = \sigma^2\text{MisEsc}_i\)
2. Power variance model: \(\sigma^2_i = \sigma^2|\text{MisEsc}_i|^{2\delta}\)
3. Exponential variance model: \(\sigma^2_i = \sigma^2e^{2\delta \text{MisEsc}_i}\)
4. Constant + power variance model: \(\sigma^2_i = \sigma^2(\delta_1 + |\text{MisEsc}_i|^{\delta_2})^2\)

varconstp <- gls(SpnEsc ~ MisEsc, 
                 weights = varConstPower(form = ~ MisEsc), 
                 data = sockeye)

See the book for syntax associated with the other models.

Standardized residuals

Standardized residuals = \((Y_i - \hat{Y}_i)/\hat{\sigma}_i\), should have approximately constant variance:

plot(varconstp)

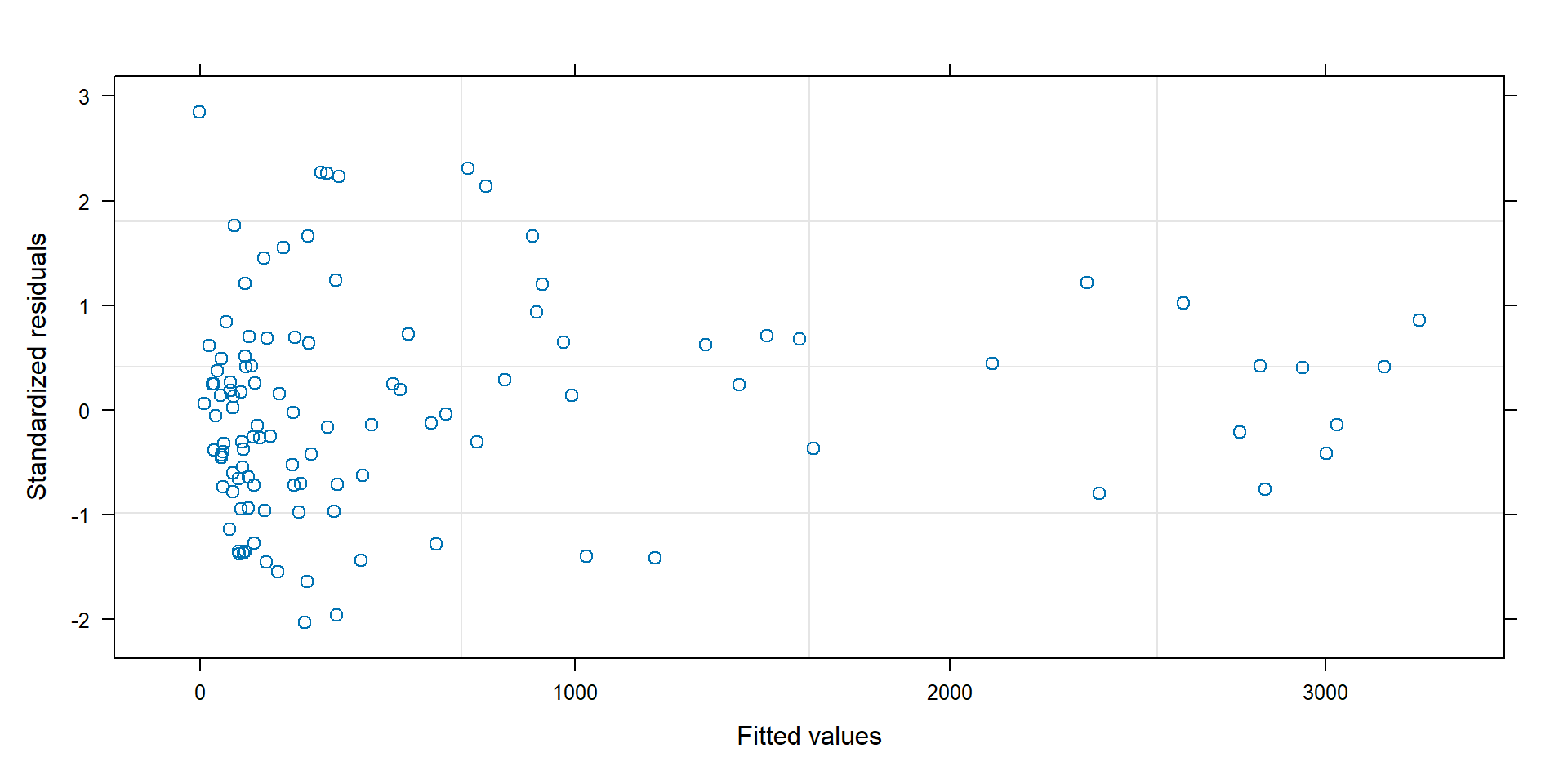
Variance depending on \(\mu_i\)

\[\begin{gather} Y_i \sim N(\mu_i, \sigma_i^2) \nonumber \\ \mu_i = \beta_0 + \beta_1X_i \nonumber \\ \sigma^2_i = \mu_i^{2\delta} \nonumber \end{gather}\]

Fit using varPower(form = ~ fitted(.)). See textbook via this link.

Zuur et al.’s Strategy (Section 4.2.3)

• Start with a “full model” (containing as many predictors as possible) fit using lm

• Inspect residuals, consider alternative variance structures if necessary
  • Inspect normalized residuals = \(\frac{Y_i-\hat{Y_i}}{\widehat{\sigma_i}}\) (these should have constant variance if the variance model is adequate)
  • Compare models using AIC (after refitting the constant variance model using gls)
  • Settle on optimal variance model

• Choose best set of predictor variables for the mean of \(Y_i\) (using the variance model, chosen above)

• Check diagnostics again and pick best model

…Try to make sense of your results.

Approximate Confidence and Prediction Intervals

For a confidence interval, we need to consider:

\(var(\widehat{E[Y_i|X_i]}) = var(\hat{\beta}_0 + X_i\hat{\beta}_1)\)

For a prediction interval, we need to consider:

\(var(\hat{Y}_i|X_i) = var(\hat{\beta}_0 + X_i\hat{\beta}_1+ \epsilon_i)\)

• Confidence interval = captures uncertainty regarding the average value of \(Y\) (given by the line)

• Prediction interval = captures uncertainty regarding a particular value of \(Y\) (need to also consider spread about the line)

Matrix Multiplication: Expected Value

\(\widehat{E[Y_i|X_i]}= \hat{\beta}_0 + \hat{\beta_1}X_i\)

\(\widehat{E[Y|X]}= \begin{bmatrix} 1 & X_1\\ 1 & X_2\\ \vdots & \vdots\\ 1 & X_n\\ \end{bmatrix}\begin{bmatrix} \hat{\beta}_0\\ \hat{\beta}_1\\ \end{bmatrix}=\begin{bmatrix} \hat{\beta}_0 + X_1\hat{\beta}_1\\ \hat{\beta}_0 + X_2\hat{\beta}_1\\ \vdots \\ \hat{\beta}_0 + X_n\hat{\beta}_1\\ \end{bmatrix}\)

Matrix multiplication: Variances

\(var(\widehat{E[Y|X]}) = Var(\hat{\beta}_0 + X\hat{\beta}_1) = Var(\hat{\beta}_0) + X^2Var(\hat{\beta}_1)+2XCov(\hat{\beta}_0, \hat{\beta}_1)\)

Define:

Let \(X\) = \(\begin{bmatrix} 1 & X_1\\ 1 & X_2\\ \vdots & \vdots\\ 1 & X_n\\ \end{bmatrix}\) and \(X^\prime\) be its transpose

\(\hat{\Sigma} =\begin{bmatrix} \hat{\sigma}^2_{\hat{\beta}_0} & \hat{\sigma}^2_{\hat{\beta}_0,\hat{\beta}_1}\\ \hat{\sigma}^2_{\hat{\beta}_0,\hat{\beta}_1} & \hat{\sigma}^2_{\hat{\beta}_1} \\ \end{bmatrix}\)

\(\widehat{var}(\widehat{E[Y|X]}) = Var(\hat{\beta}_0 + \hat{\beta}_1X)\) = \(X\hat{\Sigma}X^\prime\)

Calculations in R

We can use matrix multiplication to efficiently calculate intervals for multiple observations.

In R, we do this by using %*%

Let \(X\) = design matrix = \(\begin{bmatrix} 1 & X_1\\ 1 & X_2\\ \vdots & \vdots\\ 1 & X_n\\ \end{bmatrix}\)

\(\widehat{E[Y|X]} = X\)%*% coef(modelname) gives us predicted values for all rows of the \(X\) matrix.

Calculations in R

\(\widehat{var}(\widehat{E[Y|X]}) = X\)%*% vcov(modelname) %*%\(t(X)\)

• vcov(model) = \(\hat{\Sigma}\) = estimated variance-covariance matrix of \(\hat{\beta}\) (works forlm, gls, maybe others)
• We use t to get a transpose of a matrix

We end up with a matrix that looks something like:

\(\begin{bmatrix} var(\hat{Y}_1) & cov(\hat{Y}_1, \hat{Y}_2) & \cdots & cov(\hat{Y}_1, \hat{Y}_n)\\ cov(\hat{Y}_2, \hat{Y}_1) & \ddots & \ddots & \vdots\\ \vdots & \ddots & \ddots & cov(\hat{Y}_{n-1}, \hat{Y}_n) \\ cov(\hat{Y}_n, \hat{Y}_1) & \cdots & cov(\hat{Y}_{n}, \hat{Y}_{n-1}) & var(\hat{Y}_n)\\ \end{bmatrix}\)

Pull off the diagonal elements (the variances) - see the textbook for code.

Prediction Intervals

\(var(\hat{Y}_i|X_i) = var(\hat{\beta}_0 + X\hat{\beta}_1+ \epsilon_i)\)

• \(var(\epsilon_i) = var(Y_i | X_i) = \sigma^2_i\) and estimated by \(\hat{\sigma}^2_i\).
• In many cases, \(\hat{\sigma}^2_i\) is independent of \(\begin{bmatrix}\hat{\beta}_0 & \hat{\beta}_1\\ \end{bmatrix}\)
• This implies \(cov(\hat{\sigma}^2_i, \hat{\beta}_0) = cov(\hat{\sigma}^2_i, \hat{\beta}_1)=0\)

So, to construct a prediction interval, we approximate \(var(\hat{Y}_i|X_i)\) with:

\(var(\hat{Y}_i|X_i) \approx \widehat{var}(\hat{\beta}_0 + X_i\hat{\beta}_1) + \hat{\sigma}^2_i\) = \(X_i\hat{\Sigma}X_i^{\prime} + \hat{\sigma}^2_i\).

Additional Notes

Note, these estimates are approximate in that:

• They rely on asymptotic normality (central limit theorem) [think difference between \(t\) and \(z\)]
• They ignore uncertainty in the variance parameters

Temporal or Spatial Correlation

\[Y_{i} = \beta_0 + \beta_1 X_{i} +\epsilon_{i}\] \[\epsilon_{i} \sim N(0, \Omega)\]

• Time series: \(cor(\epsilon_i, \epsilon_j) = \rho^{|t_i-t_j|}\)

• Spatial data: \(cor(\epsilon_i, \epsilon_j)\) depends on distance between points.

If these interest you, I highly recommend taking Brian Aukema’s class.