The Role of Probability in Regression Models

FW8051 Statistics for Ecologists

Learning Objectives

Understand the role of random variables and common statistical distributions in formulating modern statistical regression models.

  • Will need to know something about other statistical distributions
  • Will need to have an understanding of basic probability theory
    • Probability rules and random variables
    • Probability mass and probability density functions
    • Expected Value and Variance
  • How to work with probability distributions in R…

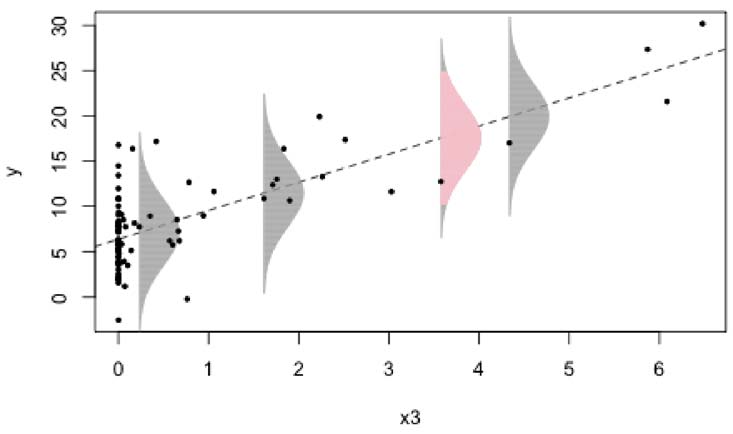
Linear Regression \(y_i = \underbrace{\beta_0 + x_i\beta_1}_\text{Signal} + \underbrace{\epsilon_i}_\text{noise}\)

Plot of normal distributions over a linear regression line to depict assumptions of linear regression.

  • Estimated errors, \(\hat{\epsilon}_i\) given by vertical distance between points and the line1
  • Find the line that minimizes the errors

Linear Regression

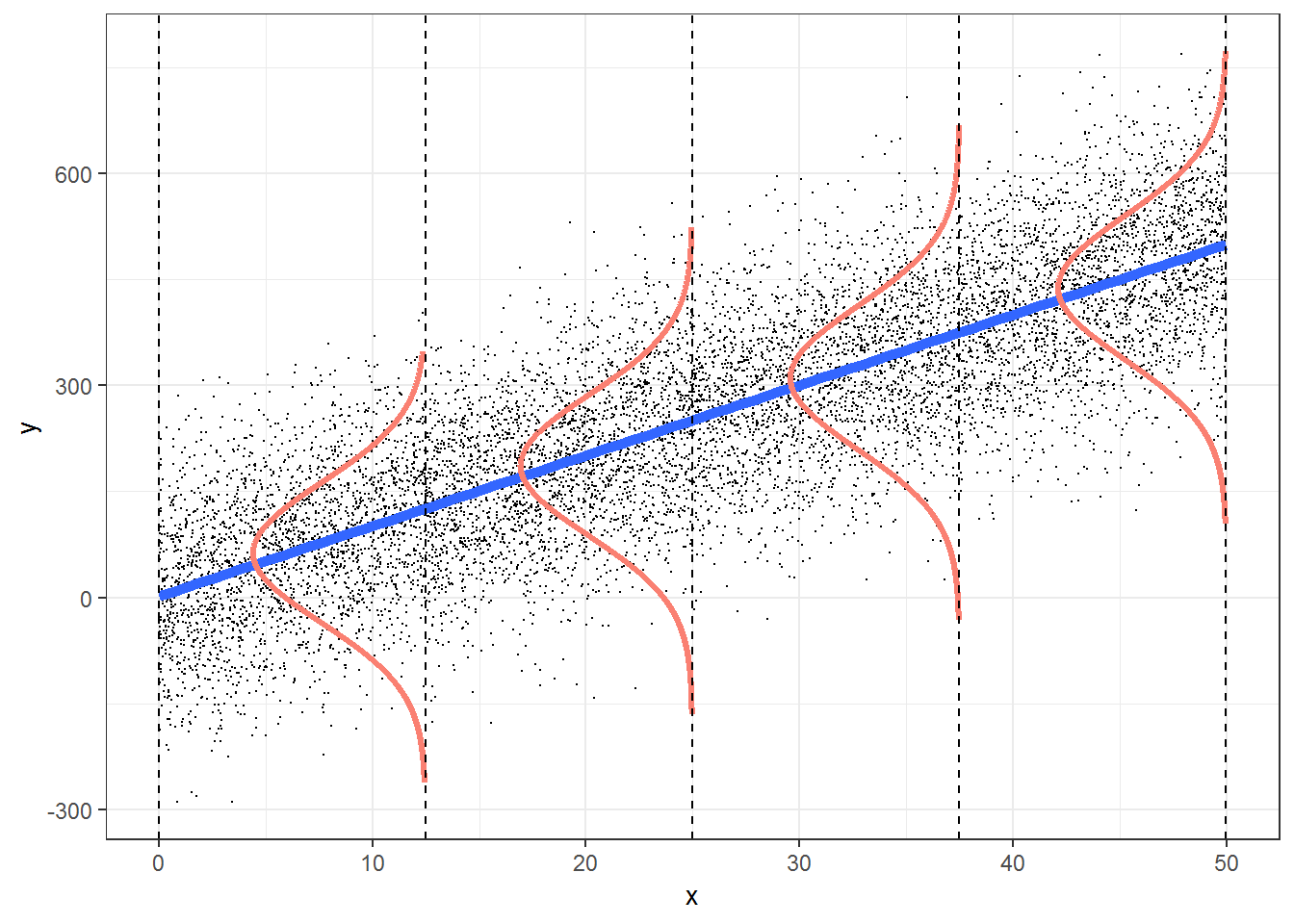
Figure illustrating the assumptions associated with simple linear regression. Scatterplot with a line and several normal distributions overlayed at different values along the x-axis.

\[Y_i \sim N(\mu_i, \sigma^2)\] \[\mu_i = \beta_0+\beta_1X_i\]

Instead of errors, think about the normal distribution as a data-generating mechanism:

  • The line gives the expected (average) value, \(\mu_i\)
  • Normal curve describes the variability about this expected value.

Generalizing to other probability distributions

Replace the normal distribution as the data-generating mechanism with another probability distribution, but which one?

It depends on the characteristics of the data

  • Does the response variable take on a continuous range of values, only integers, or is it a categorical variable taking on only 1 of 2 values?

Before we learn about different distributions, we need to know a bit more about how we measure probabilities!

Random variables

A random variable is a mapping that takes us from random events to random numbers.

Discrete Random Variables can take on a finite (or countably infinite1) set of possible values.

  • Number of birds seen on a plot {0, 1, 2, …}
  • Whether or not a moose calf survives its first year {yes, no} \(\rightarrow\) {0, 1}

Continuous Random variables take on random values within some interval.

  • T = the age at which a randomly selected white-tailed deer dies (0, \(\infty\))
  • W = Mercury level (ppm) in a randomly chosen walleye from Lake Mille Lacs [0, \(\infty\))
  • (x, y) such that x,y falls within the continental US

Discrete random variables

Probability Mass Function

A probability mass function, \(p(x)\), assigns a probability to each value that a discrete random variable, \(X\), can take on.

  • Flip a coin twice, with the following possible random events: {HH, TH, HT, TT}
  • Let \(X\) be a discrete random variable that counts the number of heads (0, 1, or 2).

Probability mass function:
x p(x)
0 1/4
1 1/2
2 1/4


Note: for any probability mass function \(\sum p(x) = 1\)

Bernoulli Distribution

Many categorical response variables can take on only one of two values (dead or alive, migrated or not, etc.)

A Bernoulli random variable, \(X\), maps the two possibilities to the numbers {0, 1} with probabilities \(1-p\) and \(p\), respectively.
x p(x)
0 1-p
1 p

\[X \sim Bernoulli(p)\]

Probability mass function:

\[p(x) = P(X = x) = p^x(1-p)^{1-x}\]

Mean of a Discrete Random Variable

The mean for a discrete random variable with probability function, p(x), is given by:

\[E[X] = \sum_{x} xp(x)\]

\[X \sim Bernoulli(p)\]
x p(x)
0 1-p
1 p
  • \(E[X] = \sum\limits_{x\in (0,1)} xp(x) =\) \(0(1-p) + 1p = p\)

Variance and Standard Deviation

The variance for a discrete random variable with probability function, p(x), and mean \(E[x]\) is given by:


\(Var(X) = E(X-E(X))^2 = \sum \limits_{x} (x-E[x])^2p(x) = E[x^2]-(E[x])^2\)


The standard deviation is \(\sigma=\sqrt{Var(x)}\)

\[X \sim Bernoulli(p)\]
x p(x)
0 1-p
1 p
  • \(Var[X] = \sum\limits_{x\in (0,1)} (x-E[x])^2p(x)\) \(=(0-p)^2(1-p) + (1-p)^2p = p(1-p)\)

Continuous random variables

Probability Density Function f(x)

\[X \sim N(\mu, \sigma^2)\]

\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

Probabilities are measured in terms of areas under the curve, \(f(x)\):

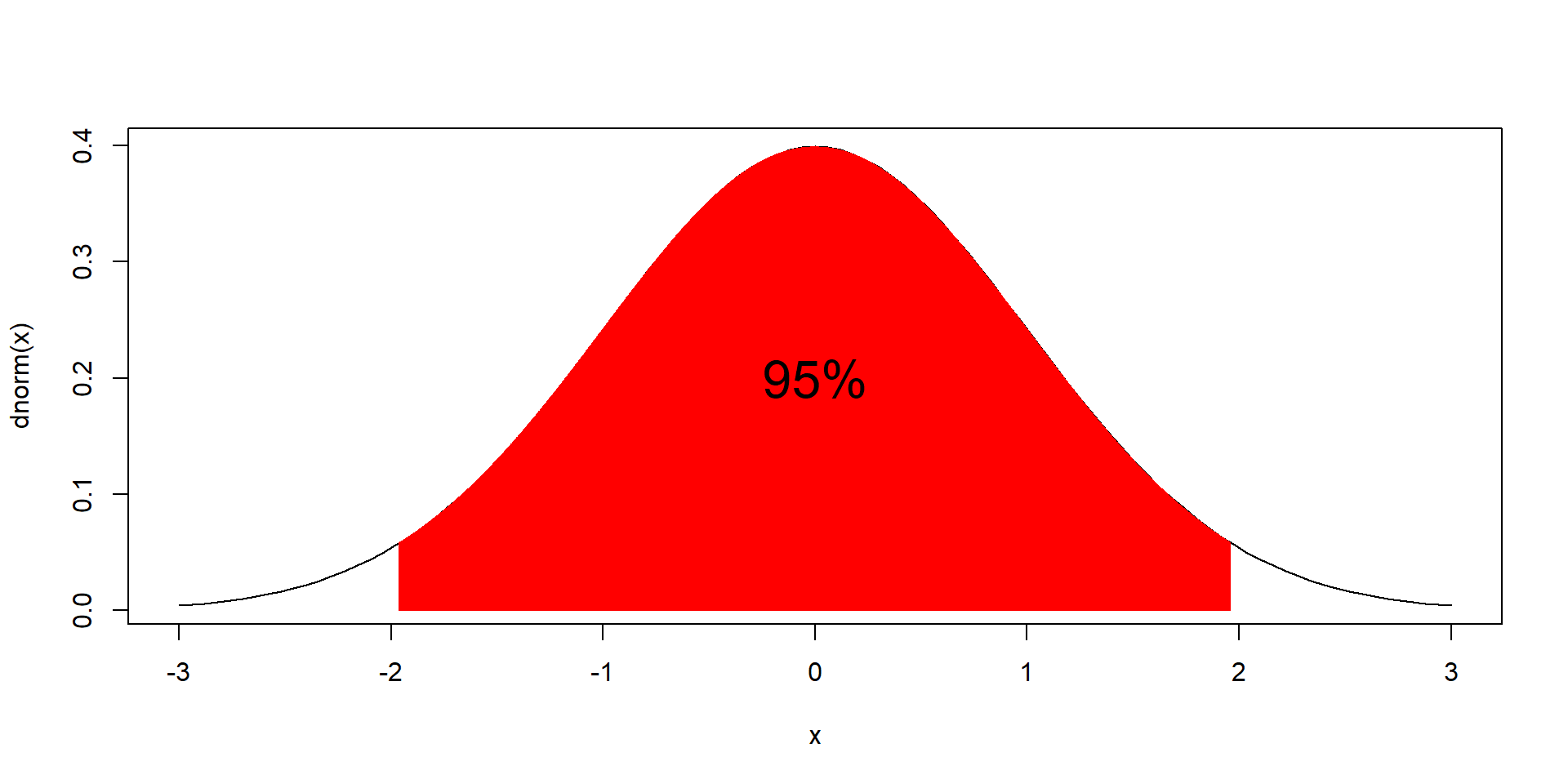
Picture of a normal distriubution, with the red shaded area associated with P(-1.96X < 1.96).

\[P(-1.96 < X < 1.96) = \int_{-1.96}^{1.96} f(x)dx = 0.95\]

  • Probability of any point, P\((X = x)\) = 0
  • P(a \(\le X \le\) b) = P(a \(< X <\) b)

Cumulative Density Function F(x)

Probability density function, \(f(X)\)

Cumulative distribution function, \(F(X) = P(X \le x)= \int_{-\infty}^{x}f(x)dx\)

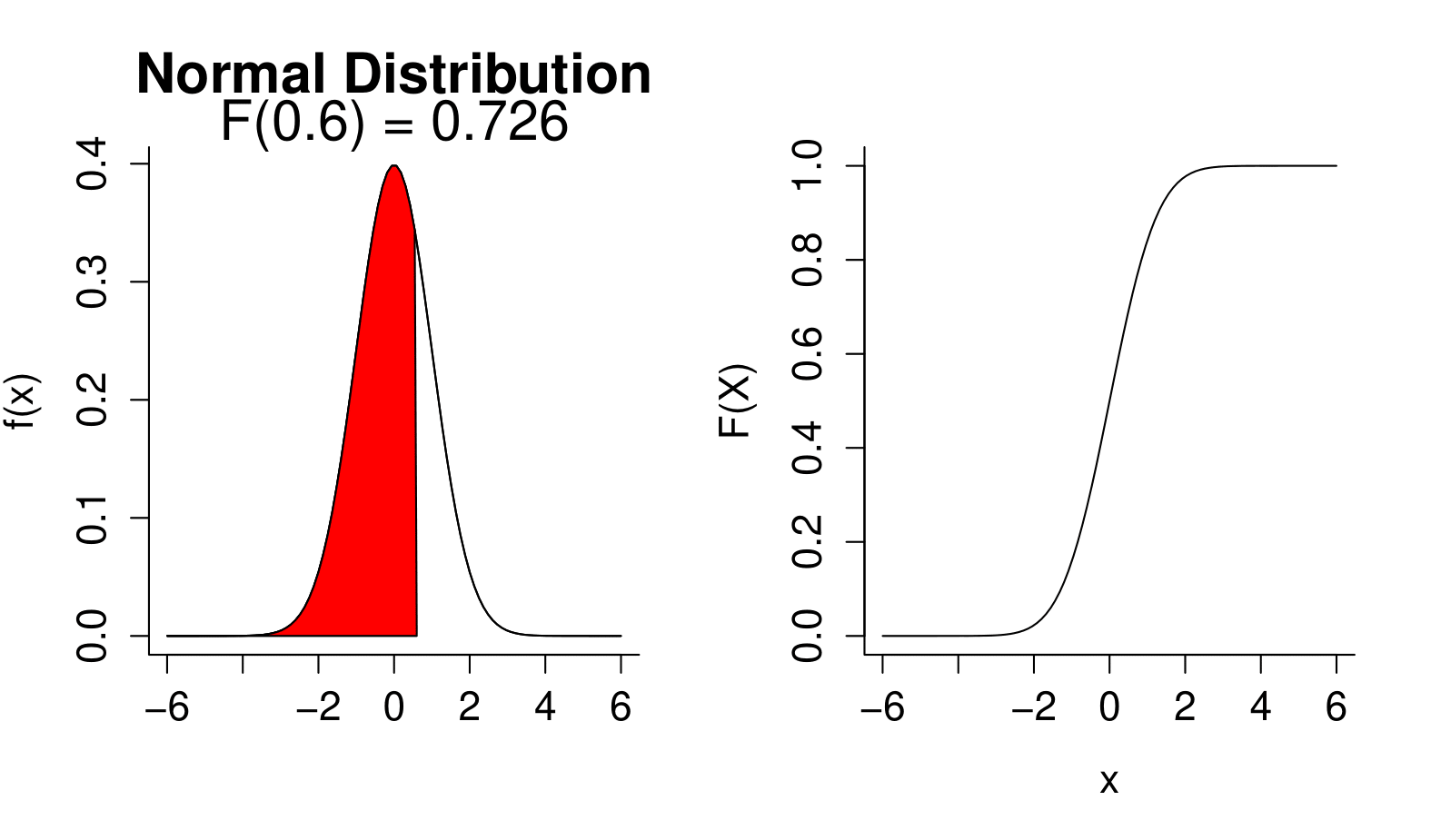
Probability density function (left) and cumulative density function (right) for a normal distriubution.
  • Unlike probabilities f(x) can be greater than 1
  • \(\int f(x)dx = 1\) (area under the curve is one)
  • \(F(x)\) goes from 0 to 1

E[X], Var[X], Continuous random variables

Replace sums with integrals!


Mean: \(E[X] = \mu = \int_{-\infty}^{\infty}xf(x)dx\)


Variance: \(Var(X) = \int_{-\infty}^{\infty}(x-E[X])^2f(x)dx\)

Distributions in R

For each probability distribution in R, there are 4 basic probability functions, starting with either - d, p, q, or r:

  • d is for “density” and returns the value of f(x) - probability density function (continuous distributions) - probability mass function (discrete distributions).

  • p is for “probability”; returns a value of F(x), cumulative distribution function.

  • q is for “quantile”; returns a value from the inverse of F(X); also know as the quantile function.

  • r is for “random”; generates a random value from the given distribution.

Functions in R

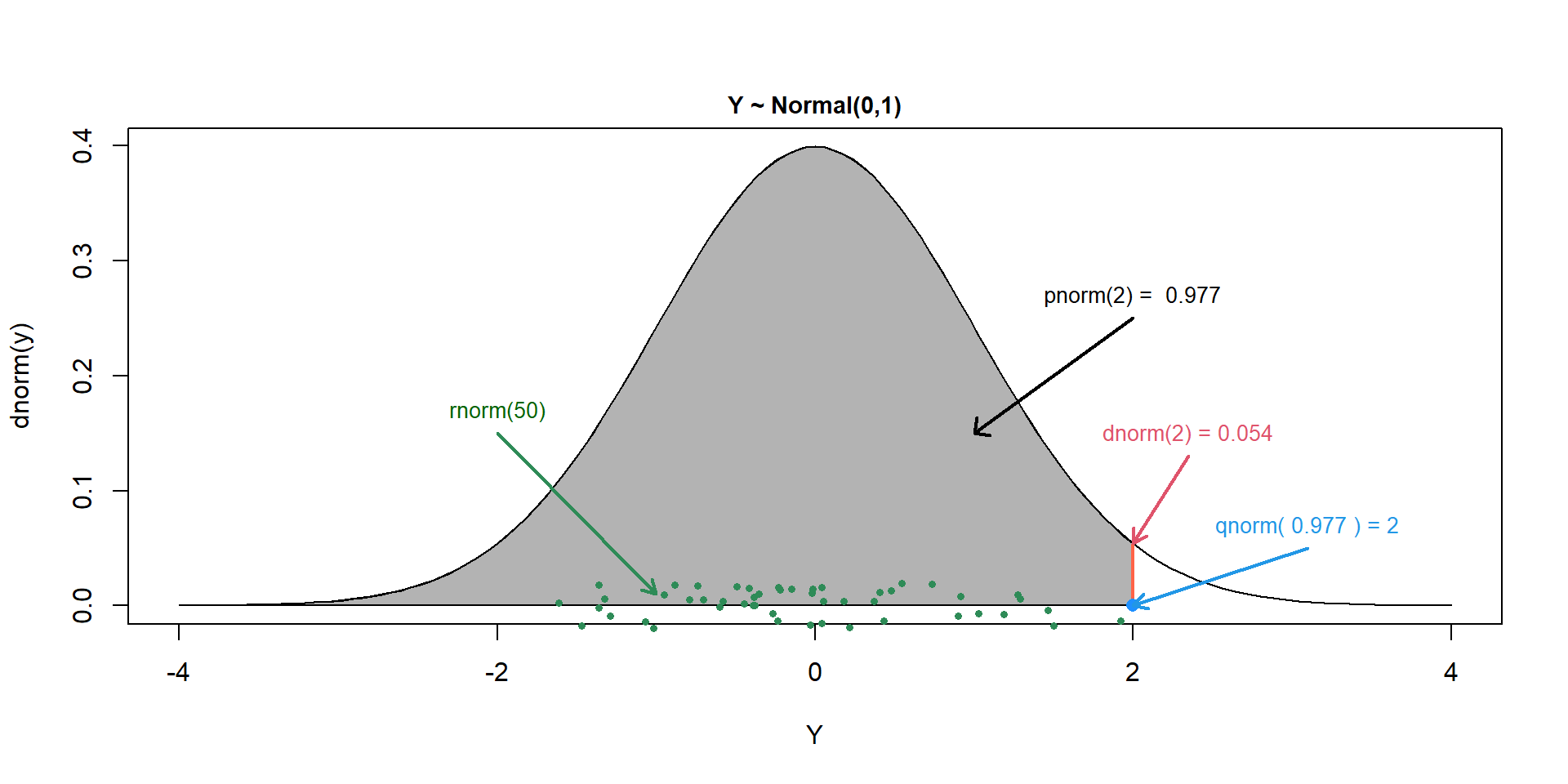
Picture of a normal distribution showing different ways to interact with it using R's built in functions, dnorm, rnorm, pnorm, and qnorm.

Use this graph, and R help functions if necessary, to complete Exercise 9.1 in the companion book.

Normal Distribution \(X \sim N(\mu, \sigma^2)\)

\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

Parameters:

  • \(\mu = E[X]\)
  • \(\sigma^2 = Var[X]\)

Characteristics:

  • Mean and variance are independent (knowing one tells us nothing about the other)…this is unique!

  • \(X\) can take on any value (i.e., the range goes from \(-\infty\) to \(\infty\)) …

  • R normal functions: dnorm, pnorm, qnorm, rnorm.

  • JAGS: dnorm

log-normal Distribution: \(X \sim\) Lognormal\((\mu,\sigma)\)

  • \(X\) has a log-normal distribution of if \(\log(X) \sim N(\mu, \sigma^2)\)
  • \(\mu\) and \(\sigma\) are the mean and variance of log(\(X\)) not \(X\)
  • Range: > 0
  • R: dlnorm, plnorm, qlnorm, rlnorm with parameters and
  • \(E[X] = \exp(\mu+ 1/2 \sigma^2)\)
  • \(Var(X)= \exp(2\mu + \sigma^2)(\exp(\sigma^2)-1)\)
  • \(Var(X) = kE[X]^2\)

Motivation for log-normal

CLT: if we sum a lot of independent things, then we get a normal distribution.

If we multiply a lot of independent things, we get a log-normal distribution, since:

\[log(X_1X_2\cdots X_n) = log(X_1)+log(X_2)+\ldots log(X_n)\]

Possible examples in biology? Population dynamic models

Lognormal Distribution

Explore briefly in R:

curve(dlnorm(x, meanlog=0,sdlog=2), from=0, to=1000)
eps<-rlnorm(10000,meanlog=0, sdlog=2)
mean(eps)
var(eps)

Compare to the expressions for the mean and variance as a function of (\(\mu, \sigma\)):

  • \(E[X] = \exp(\mu+ 1/2 \sigma^2)\)
  • \(Var(X)= \exp(2\mu + \sigma^2)(\exp(\sigma^2)-1)\)

Bernoulli Distribution:

\[X \sim Bernoulli(p)\]

\[f(x) = P(X = x) = p^X(1-p)^{1-x}\]

  • One parameter, \(p\), the probability of ‘success’ = \(P(X=1)\)
    • \(0 \le p \le 1\)
  • \(E[X] = p\)
  • \(Var[X] = p(1-p)\)
  • JAGS and WinBugs: dbern
  • R has only Binomial distribution (next)

Binomial random variable: \(X \sim\) Binomial\((n,p)\)

A binomial random variable counts the the number of “successes” (any outcome of interest) in a sequence of trials where

  • The number of trials, n, is fixed in advance
  • The probability of success, p, is the same on each trial
  • Successive trials are independent of each other

Formally, a binomial random variable arises from a sum of independent Bernoulli random variables, each with parameter, \(p\):

\[Y = X_1+X_2+\ldots X_n\]

Binomial Probability Function

For a binomial random variable with n trials and probability of success p on each trial, the probability of exactly k successes in the n trials is:


\(P(x = k) ={n \choose k}p^k(1-p)^{n-k}\)

\({n \choose k} = \frac{n!}{k!(n-k)!}\) with \(n!\) = \(n(n-1)(n-2) \cdots (2)1\)

  • \(E[X] = np\)
  • \(Var(X) = np(1-p)\)
  • In R: dbinom, pbinom,qbinom,rbinom
  • size = \(n\) and prob = \(p\) when using these functions.

Free Throws

Raymond Felton’s free throw percentage during the 2004-2005 season at North Carolina was 70%. If we assume successive attempts are independent, what is the probability that he would hit at least 4 out of 6 free throws in 2005 Championship Game (he hit 5)?

Picture of Rayond Felton with a picture of Ray Fieberg as a baby in the corner.

\(P(X \ge 4) = P(X=4) + P(X=5) + P(X=6)\)

\(= {6 \choose 4}0.7^{4}0.3^2 + {6 \choose 5}0.7^{5}0.3^1 + 0.7^{6}\)

choose(6,4)*(0.7)^4*(0.3)^2+choose(6,5)*(0.7)^5*(0.3)+
  0.7^6
[1] 0.74431
sum(dbinom(4:6, size=6, p=0.7))
[1] 0.74431
pbinom(3, size=6, p=0.7,lower.tail=FALSE)
[1] 0.74431

Multinomial Distribution

\[X \sim Multinomial(n, p_1, p_2, \ldots, p_k)\]

  • Records the number of events falling into each of \(k\) different categories out of \(n\) trials.
  • Parameters: \(p_1, p_2, \ldots, p_k\) (associated with each category)
  • \(p_k = 1-\sum_{i-1}^{k-1}p_i\)
  • Generalizes the binomial to more than 2 (unordered) categories
  • R: dmultinom, pmultinom, qmultinom, rmultinom.
  • JAGS: dmulti

Multinomial distribution

\(X = (x_1, x_2, \ldots, x_k)\) a multivariate random variable recording the number of events in each category


If \((n_1, n_2, \ldots, n_k)\) is the observed number of events in each category, then:


\(P((x_1, x_2, \ldots, x_k) = (n_1, n_2, \ldots, n_k)) = \frac{n!}{n_1!n_2! \cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k}\)

Poisson Distribution: \(N_t \sim Poisson(\lambda)\)

Let \(N_t\) = number of events occurring in a time interval of length \(t\). What is the probability of observing \(k\) events in this interval?

\[P(N_t = k) = \frac{\exp(-\lambda t)(\lambda t)^k}{k!}\]

Events in 2-D space, if events occur at a constant rate, the probability of observing \(k\) events in an area of size \(A\):

\[P(N_A = k) = \frac{\exp(-\lambda A)(\lambda A)^k}{k!}\]

If \(A\) or \(t\) is constant:

\[P(N = k) = \frac{\exp(-\lambda )(\lambda)^k}{k!}\]

Poisson distribution

  • Single parameter, \(\lambda\) = lambda.
  • \(E[X] = Var(X) = \lambda\)
  • R: dpois, ppois, qpois, and rpois.
  • JAGS: dpois

Examples:

  • Spatial statistics (null model of “complete spatial randomness”“)
  • Can be motivated by random event processes with constant rates of occurrence in space or time

Poisson distribution

Suppose a certain region of California experiences about 5 earthquakes a year. Assume occurrences follow a Poisson distribution. What is the probability of 3 earthquakes in a given year?

dpois(3, lambda=5)
[1] 0.1403739
5^3*exp(-5)/(3*2) 
[1] 0.1403739

Geometric Distribution

Number of failures until you get your first success.

\[f(x) = P(X = x) = (1-p)^xp\]

  • Parameter = \(p\) (probability of success)
  • Range: {0, 1, 2, …}
  • \(E[X] = \frac{1}{p} -1\)
  • \(Var[X] = \frac{(1-p)}{p^2}\)
  • *geom

Negative Binomial: Classic Parameterization

\(X_r\) = Number of failures, \(x\), before you get \(r\) successes; \(X_r \sim\) NegBinom(\(p\))

  • Total of \(n = x+r\) trials
  • Last trial is a success (\(p\))
  • The preceding \(x+r-1\) trials had \(x\) failures (equiv. to a binomial experiment)

\(P(X = x) = {x+r-1 \choose x}p^{r-1}(1-p)^xp\)

or

\(P(X = x) = {x+r-1 \choose x}p^{r}(1-p)^x\)

  • \(E[X] = \frac{r(1-p)}{p}\)
  • \(Var[X] = \frac{r(1-p)}{p^2}\)

Ecological Parameterization

Express \(p\) in terms of mean, \(\mu\) and \(r\):

\[\mu = \frac{r(1-p)}{p} \Rightarrow p = \frac{r}{\mu+r} \text{ and }\]

\[1-p = \frac{\mu}{\mu+r}\]

Plugging these values in to \(f(x)\) and changing \(r\) to \(\theta\), we get:

\(P(X = x) = {x+\theta-1 \choose x}\left(\frac{\theta}{\mu+\theta}\right)^{\theta}\left(\frac{\mu}{\mu+\theta}\right)^x\)

Then, let \(\theta\) = dispersion parameter take on any positive number (not just integers as in the original parameterization)

Negative Binomial: \(X \sim\) NegBin(\(\mu, \theta\))

\(P(X = x) = {x+\theta-1 \choose x}\left(\frac{\theta}{\mu+\theta}\right)^{\theta}\left(\frac{\mu}{\mu+\theta}\right)^x = \frac{(x+\theta-1)!}{x!(\theta-1)!}\left(\frac{\theta}{\mu+\theta}\right)^{\theta}\left(\frac{\mu}{\mu+\theta}\right)^x\)

  • \(E[X] = \mu\)
  • \(Var(X) = \mu + \frac{\mu^2}{\theta}\)
  • In r: *nbinom, with parameters (prob = p, size = \(n\)) or  (mu = \(\mu\), size = \(\theta\))
  • JAGS: dnegbin with parameters (\(p\), \(\theta\))

Overdispersed relative to Poisson (Var(x)/E[x] = 1 + \(\frac{\mu}{\theta}\)) versus 1 for Poisson

Poisson is a limiting case (when \(\theta \rightarrow \infty\))

Negative Binomial

Its appeal for use as a probability generating mechanism in ecology includes the following.

  • Allows for non-constant variance typical of count data.
  • It often fits zero-inflated data well (and much better than a Poisson distribution).
  • It respects the discreteness of the data (no need to transform).
  • It can be motivated biologically - e.g.:

If: \(X_i \sim\) Poisson(\(\lambda_i\)), with \(\lambda_i \sim\) Gamma(\(\alpha,\beta\)), then \(X_i\) has a negative binomial distribution.

Continuous Uniform

If observations are equally likely within an interval (A,B):

\[f(x) = \frac{1}{b-a}\]

  • Two parameters (a, b)
  • Model of ignorance for prior distributions
  • \(E[X] = (a+b)/2\)
  • \(Var(X) = \sqrt{(b-a)^2/12}\)
  • *unif
  • JAGS: dunif(lower, upper)

Gamma Distribution: \(X \sim\) Gamma(\(\alpha, \beta\))

\[f(x) = \frac{1}{\Gamma(\alpha)}x^{\alpha-1}\beta^\alpha\exp(-\beta x)\]

  • Range 0 to \(\infty\)
  • \(\Gamma(\alpha)\) is a generalization of the factorial function (!) that we’ve seen earlier
  • \(\alpha\) and \(\beta\) are parameters \(>\) 0.
  • \(E[X] = \frac{\alpha}{\beta}\)
  • \(Var[X] =\frac{\alpha}{\beta^2}\)
  • R: *gamma

Beta Distribution: \(X \sim\) Beta(\(\alpha, \beta\))

\[f(x) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}\]

  • ranges from 0 to 1.
  • \(\alpha\) and \(\beta\) are parameters \(>\) 0.
  • \(E[X] = \frac{\alpha}{\alpha+\beta}\)
  • \(Var[X] =\frac{\alpha}{(\alpha+\beta)^2(\alpha+\beta+1)}\)
  • R: *beta

Exponential: \(X \sim\) Exp(\(\lambda\))

\[f(x) = \lambda \exp(-\lambda x)\]

  • Range 0 to \(\infty\)
  • \(\lambda > 0\)
  • \(E[X] = \frac{1}{\lambda}\)
  • \(Var[X] =\frac{1}{\lambda^2}\)
  • R: *exp

Distributions

How do we choose an appropriate distribution for our data?

  • Presence-absence (0,1) at M sites \(\rightarrow\) Bernoullli/Binomial distribution
  • Counts, fixed number of sites/trials/etc \(\rightarrow\) Binomial distribution
  • Counts, in a fixed unit of time, area
    • Normal distribution if the counts are large
    • Poisson distribution: if \(E[Y |X] \approx Var(Y|X)\)
    • If \(Var(Y|X) > E(Y|X)\): Negative Binomial, Quasipoisson, Poisson-normal model
  • Continuous response variable: normal distribution (usual default)
    • gamma (if \(Y\) must be \(> 0\))
    • lognormal (if skewed data)
  • Time to event: exponential, Weibull
  • Cicular data (\(-\pi, \pi\)): von Mises

Other useful information

For a diagram showing links between distributions, see:

Diagram of distribution relationships

Want to visualize different statistical distributions, check out this link.

Note that some can be written in multiple ways:

For example, gamma:

\[f(x) = \frac{1}{\Gamma(\alpha)}x^{\alpha-1}\beta^\alpha \exp(-\beta x)\]

\[f(x) = \frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}\exp(-x/\beta)\]