Delta Method

FW8051 Statistics for Ecologists

Learning Objectives

Understand how we can use the delta method to calculate SEs for functions of parameters

See also:

In the GLS section, we learned how to calculate \(var(\hat{\beta}_0 + X_i\hat{\beta}_1)\) using matrix multiplication:

\[\text{var}(X\beta) = X\Sigma X^T\]

where \(X\) is our design matrix, \(\Sigma\) is the var/cov matrix of our parameters:

\(X = \begin{bmatrix} 1 & X_1\\ 1 & X_2\\ \vdots & \vdots\\ 1 & X_n\\ \end{bmatrix}\) \(\Sigma = \begin{bmatrix} \sigma^2_{\hat{\beta}_0} & \sigma^2_{\hat{\beta}_0,\hat{\beta}_1}\\ \sigma^2_{\hat{\beta}_0,\hat{\beta}_1} & \sigma^2_{\hat{\beta}_1} \\ \end{bmatrix}\)

• \(\sigma^2_{\hat{\beta}_0}, \sigma^2_{\hat{\beta}_1}\) = variance of \(\hat{\beta}_0\), \(\hat{\beta}_1\), respectively
• \(\sigma^2_{\hat{\beta}_0,\hat{\beta}_1}\) = covariance of \(\hat{\beta}_0\) and \(\hat{\beta}_1\)

What if we are interested in non-linear functions of parameters?

\[Length_i = L_\infty(1-\exp(-k Age_i))\]

Options:

• Bootstrap
• Delta method
• Baysian inference

\[Length_i = L_\infty(1-\exp(-k Age_i))\]

If we estimate \(\theta =(L_\infty, k)\) using Maximum likelihood, and our sample size is large, we know:

\[\hat{\theta} \sim MVN(\theta, I^{-1}(\theta)) \text{ with: }\]

• I(\(\theta) = \left[-\frac{\partial^2 logL(\theta)}{\partial \theta^2}\right]\) is the Hessian matrix associated with the negative log likelihood.

What if we want to calculate a confidence interval for the length at a particular age, \(Age_i\):

\(var[f(\hat{L}_\infty, \hat{k})] = var(\hat{L}_\infty(1-\exp(-\hat{k} Age_i)))\)

Delta Method

Taylors series:

\(f(\hat{\theta}) \approx f(\theta) + f'(\theta)(\theta - \hat{\theta})\) \(\implies \widehat{var(f(\theta))} \approx f'(\theta)\Sigma f'(\theta)^T |_{\theta=\hat{\theta}}\)

Let:

• \(f(L_\infty, k) = L_\infty(1-\exp(-k Age_i))\)
• \(f'(L_\infty, k) = (\frac{\partial f}{\partial L_\infty}, \frac{\partial f}{\partial k}) = (1-\exp(-k Age_i), L_\infty Age_i \exp(-kAge_i))\)
• \(\Sigma\) be the asympototic variance/covariance matrix of \((L_\infty, k)\) given by the inverse of the Hessian matrix

Delta Method

\(var(\hat{L}_\infty(1-\exp(-\hat{k} Age_i))) \approx f'(\hat{L}_\infty, \hat{k})\Sigma f'(L_\infty, k)^T|_{L_\infty = \hat{L}_\infty, k=\hat{k}}\)

Implementation

In R:

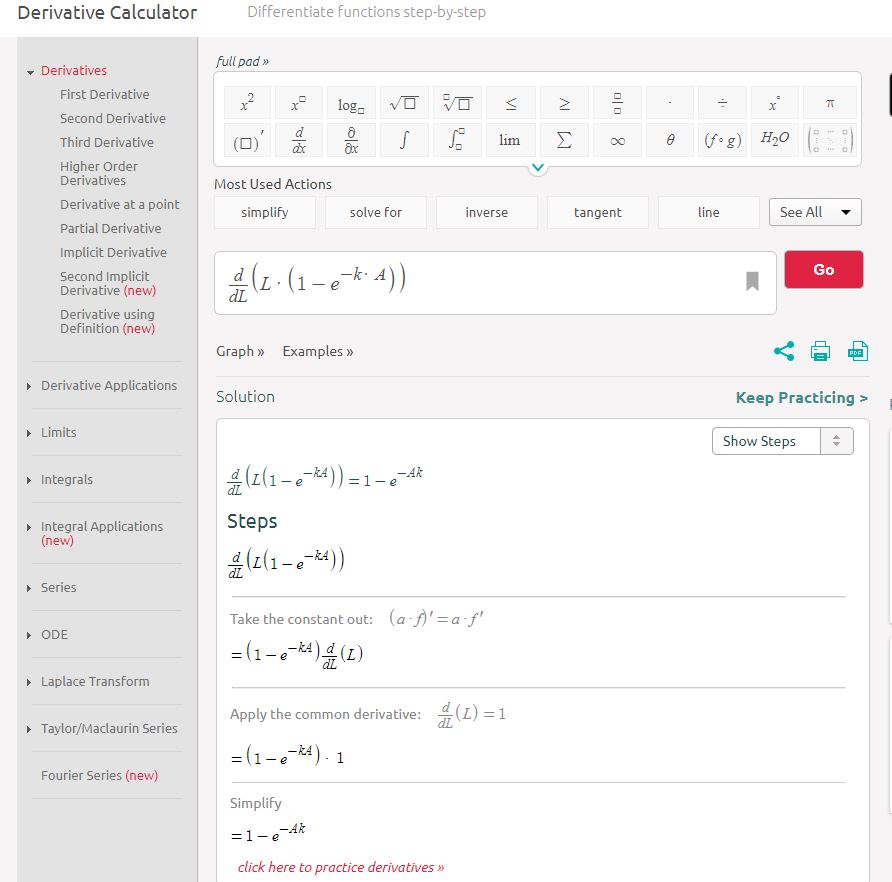
• use the deltavar function in the emdbook package to calculate the derivatives and variance; see Section 10.8 in the book
• or, calculate the derivatives yourself (or using https://www.symbolab.com/solver/derivative-calculator), then roll your own with %*% for matrix multiplication.

Derivatives